Quake3World

This is probably something everyone should consider doing, fix the texture stretching that appears on the 45° side when cutting a brush.
I just drew this little guide - Since maps with this (minor) graphical issue keeps coming all the time. Very few seems to even think about it.

Last level I was looking at was phantazm11s phantq3dm1 (just needed a recent example, it's a great level), which has this error - but one can easily find hundreds of levels...


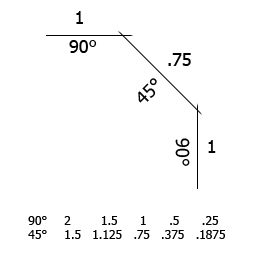(I guess the formula is 3/4 of the 90° scale - unless I'm wrong =))



Really, galls, I have nothing to do at work right now...

Yes, often a good idea, though it depends on the texture. Textures with seams (like floor tiles or something) would look weird being split in the middle of the texture. Though I suppose you can compensate with additional trim or a different texture altogether.

Ofc, I mean, you don't want a ugly seam or something there...
The level designer probably knows what looks best in the end...

>I guess the formula is 3/4 of the 90° scale

i think formula is stretch_N = stretch_90 * sin (N) or more right stretch_0 * cos (N)

Shouldn't it be the long face length of the triangle formed by 2 1 unit faces at 90 degrees to one another? So sqrt(1 + 1).

Then because that's how much longer the face is we scale the texture by:
1/(sqrt 2) = 0.707 to 3 sig. fig.

yup

.707 = sin 45 = cos 45 = 1/(sqrt 2)

extone's formula will get the stretch values for any angle

Can you translate this into some kind of example, for those that skipped a math class, or all...

The pythagorean theorem states that:
a squared + b squared = c squared.

C is the longest side of the triangle.
A and B are the adjacent sides.

So lets say the non stretched textured sides are A and B. They both have a length of 2 units.

2 squared is 4.

4 + 4 = 8 so basically we're saying the square root of a and b added together = the square root of 8.

This means the non stretched sides have 2 units that the texture needs to be applied to while the stretched, 45 degree side has 2.83 units to be applied to.

Im editing this because this theorem may not be appropriate for the purpose of this issue even if it does work for explaining the slightly skewed textures on non-axial planes.

:mathfacepalm:

Everyone is right, no one is wrong, we have two formulas that describe the same scenario.

The Pythagorean Theorem works perfectly fine in this case alone where you have a right-angle triangle and want to find the length of the longest side.

Extone's sine/cosine formula can be used to find the length of ANY angled slope, be it a 45° slope or a 72.683° slope.

But punching in 0.707... is hard and may end up looking weird, so rounding that up to a nice fractionable number like 0.75 like in Hipshot's chart is a good approximation.


Now if anyone can come up with a formula for texturing a face that has been cut using a 3-point clip, I'll be impressed because I clearly wasn't paying enough attention back in school to be able to do that still.

was going to say the same thing about punching in .707. it may look odd with some textures that repeat, so using something with a nice fraction may give better results.

of course, it's quite possible to do the reverse, and stretch the non-45° textures by 1.5 instead of 1.414 =)